تابش جسم سیاه چیست؟ راز پنهان در دل نور

در قرن نوزدهم، نظریه موجی نور که معادلات ماکسول به خوبی آن را تبیین می‌کردند، به نظریه غالب در این زمینه تبدیل شد و نظریه ذره‌ای نیوتن را که در توضیح بسیاری از پدیده‌ها با شکست مواجه شده بود، کنار زد. اما این نظریه نیز با چالش‌هایی روبرو شد. یکی از مهم‌ترین این چالش‌ها، توضیح تابش حرارتی بود.

تابش حرارتی نوعی از تابش الکترومغناطیسی است که از اجسام به دلیل دمای آن‌ها ساطع می‌شود. در واقع، هر جسمی که دمایی بالاتر از صفر مطلق داشته باشد، از خود امواج الکترومغناطیسی منتشر می‌کند. بررسی و تبیین این پدیده، به یکی از مسائل مهم و چالش‌برانگیز در دنیای فیزیک تبدیل شد.

آزمایش تابش حرارتی: روش اندازه‌گیری

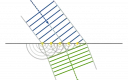
برای بررسی تابش حرارتی، می‌توان دستگاهی را آماده کرد که قادر به تشخیص تابش‌های ساطع شده از یک جسم با دمای ثابت (T1) باشد. از آنجایی که جسم گرم در تمام جهات تابش می‌کند، باید از نوعی محافظ استفاده کرد تا تابش مورد بررسی، به صورت یک باریکه باریک درآید.

با قرار دادن یک محیط پراکنده ساز (مانند منشور) بین جسم و آشکارساز، طول موج‌های (λ) تابش با زاویه (θ) پراکنده می‌شوند. از آنجایی که آشکارساز یک نقطه هندسی نیست، محدوده‌ای از زوایا (δθ) را اندازه‌گیری می‌کند که متناظر با محدوده‌ای از طول موج‌ها (δλ) است. البته، در یک آزمایش ایده‌آل، این محدوده نسبتاً کوچک است.

اگر I نشان‌دهنده شدت کل تابش در تمام طول موج‌ها باشد، شدت تابش در بازه δλ (بین λ و δλ) به صورت زیر خواهد بود:

δI = R(λ) δλ

در این معادله، R(λ) تابناکی یا شدت تابش در واحد طول موج است. با استفاده از نمادگذاری حساب دیفرانسیل و انتگرال، مقادیر δ به حد صفر میل می‌کنند و معادله به شکل زیر در می‌آید:

dI = R(λ) dλ

در آزمایش فوق، مقدار dI اندازه‌گیری می‌شود و از این طریق، می‌توان مقدار R(λ) را برای هر طول موج دلخواه تعیین کرد. این روش به ما امکان می‌دهد تا طیف تابش حرارتی یک جسم را به دقت بررسی کنیم.

تابناکی، دما و طول موج: ارتباط کلیدی

با انجام آزمایش تابش حرارتی در دماهای مختلف، مجموعه‌ای از منحنی‌های تابناکی بر حسب طول موج به دست می‌آید که نتایج قابل توجهی را نشان می‌دهند:

• افزایش دما، افزایش شدت کل تابش: شدت کل تابش در تمام طول موج‌ها (یعنی مساحت زیر منحنی R(λ)) با افزایش دما، افزایش می‌یابد.

این نتیجه کاملاً قابل انتظار است. در واقع، با محاسبه انتگرال معادله شدت تابش، به مقداری می‌رسیم که متناسب با توان چهارم دما است. این تناسب از قانون استفان-بولتزمن به دست می‌آید و با ثابت استفان-بولتزمن (σ) به شکل زیر بیان می‌شود:

I = σ T4

• کاهش طول موج ماکزیمم با افزایش دما: مقدار طول موج (λmax) که در آن تابناکی به حداکثر مقدار خود می‌رسد، با افزایش دما کاهش می‌یابد.

نتایج آزمایش‌ها نشان می‌دهد که طول موج ماکزیمم با دما رابطه معکوس دارد. در حقیقت، اگر λmax و دما را در هم ضرب کنیم، یک مقدار ثابت به دست می‌آید که به قانون جابجایی وین معروف است:

λmax T = 2.898 x 10-3 mK

تابش جسم سیاه: ساده‌سازی مسئله

توصیفات قبلی تا حدی با ساده‌سازی همراه بود. از آنجایی که نور از سطوح اجسام بازتاب می‌شود، آزمایش توصیف شده با این مشکل روبرو است که دقیقاً چه چیزی در حال اندازه‌گیری است. برای ساده‌سازی این وضعیت، دانشمندان به سراغ جسم سیاه رفتند.

جسم سیاه جسمی است که هیچ نوری را بازتاب نمی‌کند و تمام نوری که به آن می‌رسد را جذب می‌کند.

یک جعبه فلزی را در نظر بگیرید که سوراخ کوچکی روی آن ایجاد شده است. اگر نور به این سوراخ بتابد، وارد جعبه می‌شود و احتمال کمی وجود دارد که دوباره به بیرون بازگردد. بنابراین، در این حالت، این سوراخ است که نقش جسم سیاه را ایفا می‌کند، نه خود جعبه. تابش حرارتی که در خارج از سوراخ آشکارسازی می‌شود، نمونه‌ای از تابش داخل جعبه خواهد بود، بنابراین برای درک آنچه در داخل جعبه رخ می‌دهد، به تحلیل بیشتری نیاز است.

فضای داخل جعبه مملو از امواج الکترومغناطیسی ایستاده است. اگر دیواره‌های جعبه فلزی باشند، تابش در داخل جعبه منعکس می‌شود و میدان الکتریکی در هر دیوار متوقف می‌شود و یک گره در هر دیوار ایجاد می‌کند.

تعداد امواج ایستاده با طول موج بین λ و dλ به صورت زیر است:

N(λ) dλ = (8π V / λ4) dλ

در این معادله، V حجم جعبه است. این رابطه را می‌توان با تحلیل امواج ایستاده و تعمیم آن به سه بعد اثبات کرد.

هر موج منفرد، انرژی kT را به تابش داخل جعبه اضافه می‌کند. از ترمودینامیک کلاسیک می‌دانیم که تابش در داخل جعبه در تعادل حرارتی با دیواره‌ها در دمای T قرار دارد. تابش توسط دیواره‌ها جذب و به سرعت دوباره ساطع می‌شود که باعث ایجاد نوساناتی در فرکانس تابش می‌شود. میانگین انرژی جنبشی حرارتی یک اتم نوسان‌کننده برابر با 0.5kT است. از آنجایی که این‌ها نوسانگرهای هارمونیک ساده هستند، میانگین انرژی جنبشی برابر با میانگین انرژی پتانسیل است، بنابراین کل انرژی برابر با kT است.

تابناکی با چگالی انرژی (انرژی در واحد حجم) u(λ) در رابطه زیر مرتبط است:

R(λ) = (c / 4) u(λ)

این رابطه با تعیین مقدار تابشی که از یک عنصر سطح در داخل حفره عبور می‌کند، به دست می‌آید.

شکست فیزیک کلاسیک: فاجعه فرابنفش

با استفاده از فیزیک کلاسیک، روابط زیر برای چگالی انرژی (u(λ)) و تابناکی (R(λ)) به دست می‌آیند:

u(λ) = (8π / λ4) kT

R(λ) = (8π / λ4) kT (c / 4) (معروف به فرمول ریلی-جینز)

با این حال، داده‌های تجربی نشان می‌دهند که تابناکی دارای یک مقدار ماکزیمم است و با کاهش طول موج (λ) به سمت صفر، تابناکی نیز کاهش می‌یابد و به صفر میل می‌کند. این در حالی است که طبق فرمول ریلی-جینز، با کاهش طول موج، تابناکی باید به بی‌نهایت میل کند.

این несоответствие بین پیش‌بینی نظری فیزیک کلاسیک و نتایج تجربی، به عنوان فاجعه فرابنفش شناخته می‌شود. این مسئله در حدود سال 1900 مشکلات جدی برای فیزیک کلاسیک ایجاد کرد، زیرا مفاهیم اساسی ترمودینامیک و الکترومغناطیس را که در استخراج این معادلات به کار رفته بودند، زیر سوال می‌برد. (شایان ذکر است که فرمول ریلی-جینز در طول موج‌های بلندتر، به نتایج تجربی نزدیک‌تر است.)

نظریه پلانک: راه‌حلی برای فاجعه فرابنفش

ماکس پلانک پیشنهاد کرد که یک اتم تنها می‌تواند انرژی را به صورت بسته‌های مجزا (کوانتا) جذب یا ساطع کند. اگر انرژی این کوانتا متناسب با فرکانس تابش باشد، در فرکانس‌های بالا، انرژی نیز به طور مشابه بزرگ خواهد شد. از آنجایی که هیچ موج ایستاده‌ای نمی‌تواند انرژی بیشتر از kT داشته باشد، این امر یک سقف موثر بر تابناکی در فرکانس‌های بالا اعمال می‌کند و بدین ترتیب فاجعه فرابنفش حل می‌شود.

طبق نظریه پلانک، هر نوسانگر فقط می‌تواند انرژی را به مقادیری برابر با مضرب صحیحی از کوانتا انرژی (ε) جذب یا ساطع کند:

E = n ε, که در آن n = 1, 2, 3, ... (تعداد کوانتا)

انرژی هر کوانتوم نیز با فرکانس (ν) تابش متناسب است:

ε = h ν

در این رابطه، h ثابت پلانک است. با استفاده از این مفاهیم، پلانک فرمولی جدید برای تابناکی جسم سیاه ارائه داد که به خوبی با نتایج تجربی سازگار بود:

(c / 4)(8π / λ4)((hc / λ)(1 / (ehc/λ kT – 1)))

پیامدها: آغاز فیزیک کوانتومی

در حالی که پلانک ایده کوانتا را برای رفع مشکلات مربوط به یک آزمایش خاص معرفی کرد، آلبرت اینشتین پا را فراتر گذاشت و آن را به عنوان یک ویژگی اساسی از میدان الکترومغناطیسی تعریف کرد. پلانک و اکثر فیزیکدانان در پذیرش این تفسیر تردید داشتند، تا اینکه شواهد قاطعی برای اثبات آن به دست آمد. این ایده، نقطه عطفی در تاریخ فیزیک بود و راه را برای توسعه فیزیک کوانتومی هموار کرد.